5. Упражнения на понимание особенностей мышления ребенка

Начиная со школы, ученик, обладающий особенностями мышления, характерными для более младшего или старшего возраста, может испытывать выраженные трудности в учебной деятельности. Педагогам необходимо уметь понимать особенности мышления как с точки зрения теории развития интеллекта Ж. Пиаже, так и с точки зрения характеристик свойств мышления по теории  Н.А. Менчинской и ее учеников, а также с точки зрения взглядов Л.С. Выготского на феномен зоны ближайшего развития и уровня актуального развития.

 Укажите, о чем (с точки зрения теории Ж. Пиаже, Н.А. Менчинской, Л.С. Выготского) свидетельствуют неправильные ответы ребенка при решении следующих задач:

1. Ребенок умеет находить значения выражений сложением столбиком двузначных чисел с переходом через десяток, например: 23 и 47, 89 и 12. Когда его просят сложить 237 и 484, он заявляет, что они «не проходили, как складывать трехзначные числа».

2. Ребенок получает 5 палочек разной длины. Его просят разложить палочки в порядке возрастания длины. Ребенок сравнивает 2 палочки между собой. Затем берет третью и сравнивает ее с каждой из предыдущих двух. Раскладывает 3 палочки в порядке возрастания длины. Затем берёт 4-ю и прикладывает ее к каждой из трех разложенных. Ищет место, куда она подходит, кладет. Затем берет 5-ю, сравнивает прикладыванием с каждой из четырёх разложенных, кладет на нужное место. Как будет действовать ребенок на следующей стадии развития интеллекта?

3. Перед ребенком раскладывают 2 ряда кружков, кружки верхнего ряда строго под кружками нижнего, чтобы показать, что кружков одинаково. Спрашивают: «Одинаково ли кружков в верхнем и нижнем рядах?» После утвердительного ответа ребенка на его глазах кружки нижнего ряда растаскивают так, что расстояние между ними значительно увеличивается на 1,5 – 2 кружка. Опять спрашивают: «А теперь?» Ребенок отвечает: «Конечно, в нижнем ряду больше, их ведь вон как длинно стало!»

4. Перед ребенком раскладывают деревянные бусины красного и желтого (их значительно больше, чем красных) цвета, просят показать бусины одного цвета, другого, убеждаются, что ребенок понимает, из чего сделаны бусины (из дерева, деревянные), и спрашивают: «Из каких бусин можно сделать более длинное ожерелье – из желтых или деревянных?» Ребенок отвечает, что из желтых, потому что их больше, это видно.

5. Перед ребенком раскладывают в ряд пластмассовых игрушечных коров, при этом у десяти коров глаза закрыты («они спят»), у других 5 открыты («они не спят»). Ребенка спрашивают: «Какое стадо больше: из спящих коров или из коров?» Как ответит ребенок с центрацией? С необратимостью?

6. Ребенку предлагается посмотреть на 2 одинаковых прямоугольника из бумаги. Затем один из прямоугольников разрезается по диагонали на 2 части. Из этих частей складывают треугольник и задают вопрос: «Одинаково ли бумаги в прямоугольнике и треугольнике?» Как ответит ребенок, находящийся по уровню развития интеллекта на стадии дооперационных структур? С какой особенностью мышления ребенка это связано?

7. Ребенка спрашивают: «Кто такой полицейский?» Он отвечает: «Это тот, кто забирает непослушных детей, но я послушный». На какой стадии развития интеллекта находится ребенок? С какой особенностью мышления ребенка это связано?

8. Охарактеризуйте чувствительность к помощи у детей при решении задачи: 3, 6, 9, 12, ... ?

Маша – решает сама, Лена – после слов: «Здесь числа расставлены по особому правилу…» Саша – после слов: «Это число получено так же, как 12 из девяти, 9 из шести, 6 из трех ...» Света – после того, как правило сформулировано и показано на примере чисел 3, 6, 9.

9. Ответьте на вопросы А, Б, В, используя таблицу

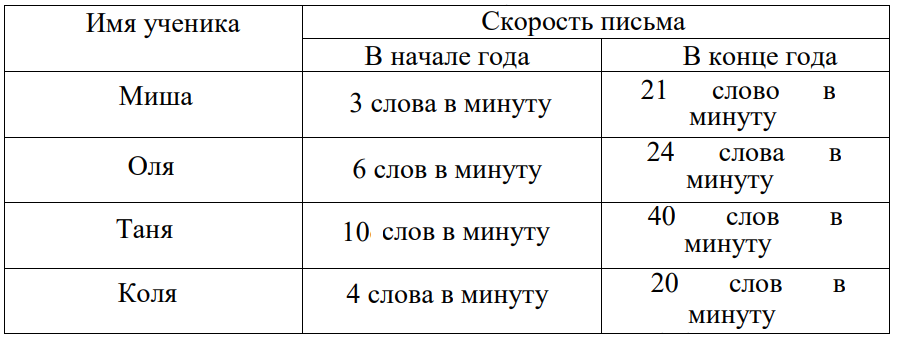
А. Кто из детей лучше учится в начале года и в конце года?

Б. У кого произошло более интенсивное развитие? Почему вы так думаете?

 В. Совпадают ли успеваемость и скорость развития письма?

10. Почему ученик начальной школы, умея складывать в столбик двузначные числа с переходом через десяток, говорит, что 4357 + 4698 он не может сложить, потому что такого они еще не проходили?

11. С какой особенностью мышления связан способ счета ребенка шести лет, который, умея складывать на палочках в пределах 10, складывает 6 + 2 так: откладывает 6 палочек одного цвета, отсчитывая их; потом откладывает еще 2 палочки другого цвета, выкладывает их следом, а затем вместо того, чтобы продолжить счет от шестой палочки 6, 7, 8, он начинает считать с самой первой палочки 1, 2, 3, 4, 5, 6 и только потом говорит 7, 8? Правильно ли поступает мама, которая ругает ребенка за такой нерациональный долгий способ счета? Что вы посоветуете родителям такого ребенка?

12. Почему дети начальной школы затрудняются при решении так называемых косвенных задач? Например: Коле 7 лет. Он младше своего брата Вити на 2 года. Сколько лет Вите?

Объясните эти трудности с точки зрения Ж. Пиаже, Н.А. Менчинской.

13. С какими особенностями мышления могут быть связаны ошибки учеников, которые выполняют такое задание:

Тема: «Различение именительного и винительного падежей имен существительных в предложении». Указать падежи всех имен существительных в предложении: «Голодный папа пришел с работы, увидел на плите грибной суп и быстро съел его».

Как предупредить ошибки?

14. Нередко ученики начальной школы плохо понимают запись вида:

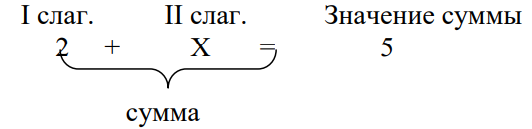
С какими особенностями мышления (по Ж. Пиаже и Н.А. Менчинской) связаны эти трудности?